Planos y rectas

recta están representado en una función y=mx+b, una función lineal donde m es diferente de cero
donde m y b son:
- m : es la pendiente... m>0, quiere decir que la función es creciente y si m<0 es decir que la función es decreciente
- b : es la coordenada en y, donde la recta corta el eje y

planos están representado mediante la ecuación ax+by+cz+d=0...
- si un punto es perpendicular a un vector, esta se halla con el producto punto del vector  y el punto
de un sistema de referencia igual a 0

Vectores

Un vector es una magnitud física definida en un sistema de referencia y tiene como características de que es una magnitud, sentido y dirección. por lo general para representa si es un vector se le agrega una flecha encima.








Operaciones que se puede realizar con los vectores.

suma y resta: dado una dos vectores que al sumar o restarla como resultado es un vector resultante






Como sumar o restar vectores?

A= (a1, a2, a3)
B=( b1, b2, b3)
R = (a1 + b1, , a2 + b2,  , a3 +  b3)

para restar es similar lo único que cambia es el signo mas por menos...

Multiplicación por escalar: al multiplicar una constante con un vector, lo que hay que tener en cuenta que la constante multiplica a todos los componentes del vector..

KA = (ka1, ka2, ka3)


Normas del vector: es el modulo o la longitud de un vector que se halla con la raiz cuadrada de la suma cuadradas de sus componentes, es decir:

un vector U=(u1, u2, u3.... un) :
||U|| =  





Vector Unitario: el vector unitario de un modulo es igual a 1

vector V = U/||U||; después hallar ||V|| = 1

Producto punto o producto escalar consiste en multiplicar componente, y sumar con la multiplicación del siguiente componente... o si tiene magnitudes y el angulo en el siguiente video se explicará explicita en como hallar el producto punto

Con el mismo producto punto entre dos vectores se es posible también hallar el angulo, que consiste en despejar la formula para hallar el ángulo entre dos vectores... en este vídeo se mostrara como hallar el angulo mediante el producto punto



En el producto punto hay tipos de ángulos es decir:

1. si el producto punto es >0 el angulo es < 90 grados : es un angulo agudo
2. si el producto punto es <0 el angulo es > 90 grados : es un ángulo obtuso
3. si el producto punto es = 0 el angulo es = 90 grados : es ortogonal

Propiedades del producto punto:

1.  el producto punto de si mismo es igual a elevarlo al cuadrado, si el vector v es diferente de cero:

2. El producto punto es conmutativo:




3. El producto punto es distributiva:







si c pertenece a los numero reales :

Producto Cruz (hallar áreas y volúmenes): también se puede expresar en determinantes teniendo en cuenta que la primera fila están los vectores unitarios i, j, k, la segunda fila es el primer vector y la segunda fila el segundo vector, ya que el producto cruz no es conmutativo; también como resultado de un producto cruz es un vector.


Propiedades del producto cruz:

Área de un paralelogramo: es la norma del producto cruz del vector u y v

Área de un triangulo: es la norma del producto cruz del vector U y V pero dividido en 2

 en el video que se muestra muestra el area de un paralelogramo y ademas halla el area de un triangulo:



















Volumen del paralelepípedo: en el paralelepípedo son 3 vectores.. ejemplo 1:

ejemplo 2 para hallar el volumen de un paralelepípedo:

  
para resolver este ejercicio primero hay que halla el producto cruz entre los vectores v y w; después hallar el producto punto

Determinantes

Para resolver un determinante es necesario tener en cuenta que sean cuadrados, es decir, de igual fila y columna

Hay varias formas de resolver los determinantes estos son:

• Cramer:

Si se presenta un determinante de 2*2 sencillamente se es necesario multiplicar la diagonal principal menos la diagonal faltante.
En el siguiente ejemplo multiplica 3*2 - (-1*5) en el numerador y en el denominador es similar


para resolver ecuaciones mediante cramer 3*3 se va haciendo un poco mas complejo por lo cual es recomendable usar método de sarrus. Sin embargo en este video se mostrará un poco de como resolver determinantes 3*3 por cramer

• Sarrus:

¿En que consiste el metodo Sarrus? Consiste en agregar dos filas o dos columnas iguales al de las primera parte, después, multiplica las diagonales principales de izquierda a derecha y resta con el resultado de derecha a izquierda... en el siguiente se hará un poco explicito de como usar el método Sarrus...

• Gauss Jordan:

Es modificar la matriz mediante suma, resta, multiplicación y división haciendo posible que la diagonal principal sea 1. También es una forma de resolver ecuaciones lineales...

PROPIEDADES DE LOS DETERMINANTES:

Propiedad 1:
El determinante de una matriz cuadrada es igual al determinante de su matriz transpuesta



Propiedad 2 : Si los elementos de una linea de una matriz se multiplican por un numero, el determinante de la matriz queda multiplicado por dicho número... en el ejemplo vemos que el 3 como constante multiplica a la prime columna del determinante..


Propiedad 3: Si todas las lineas de una matriz orden n están multiplicados por un mismo número t, el determinante de la matriz queda multiplicado por t^n... en el ejemplo todos son multiplos de 3 por lo tanto el determinante queda multiplicado por 3 que es t y n = 2..

Propiedad 4:
hacer equivalente una matriz con otra con operación aritmética y sumarlo

Propiedad 5: El determinante del producto de dos matrices cuadradas es igual al producto de los determinantes de ambas matrices




Propiedad 6: Si se cambian dos filas o dos columnas es obligatorio el determinante cambia de signo. en este ejemplo cambia la primera y segunda columna...





Propiedad 7: si una matriz tiene dos filas iguales; su determinante es 0... en el ejemplo la primera y la tercera fila son igual fila... o también cuando la suma de la primera y segunda es igual a la tercera el resultado es igual a 0... O cuando si una matriz mediante una combinación lineal es igual a cero el determinante es igual a cero.

Teoría de Grafos

DEFINICIÓN

La teoría de grafos es un conjunto de vértices que están unidas mediante aristas. En la imagen vemos 6 vértices y 7 arista...
Artista incidente : cuando un vértice une a otro vértice
Arista Aislado: Es un vértice de grado 0
Vértice pendiente: Es aquel grafo que contiene una arista


TIPOS DE GRAFOS:

• Cruce:

• Grafo sencillo o simple:

• Grafo completo: Un grafo completo si contiene un grado igual a n -1 donde n es igual al numero de vértices que compone el grafo... Para saber cuantos arista contiene un grafo completo se aplica la formula: A = (n*1(n-1))/2

• No dirigidos: Son arista que no están orientados es decir no tienen flecha

• Dirigidos: Son arista que están orientados, mediante flecha

• Grafo no simple: son grafos no dirigidos que tiene lados paralelos o lazos

• Grado o valencia de un vértice:

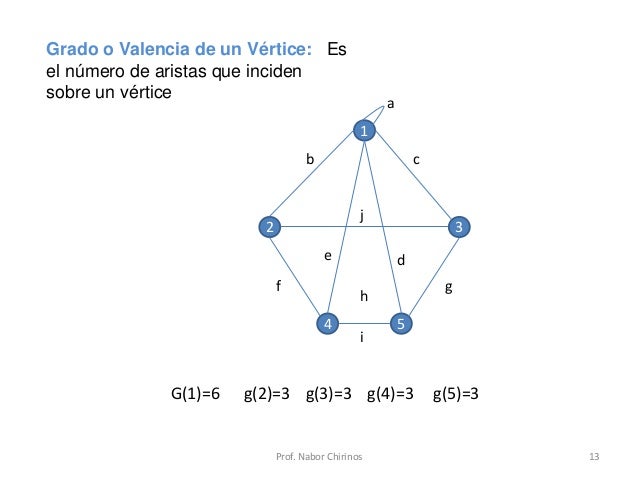
• Grado Regular: Es la misma cantidad de arista en cada vértice

En la imagen hay 4 vértices y en cada vértice hay 3 arista

• Grafo a matriz:

Matrices

Que es: Es un arreglo bidimensional en filas y columna para hallar la solución de un problema

Matrices identidad: es una matriz cuya diagonal principal es igual a 1, teniendo en cuenta que la matriz sea de igual tamaño de filas y columnas. Las matrices identidad van en orden es decir I1, I2, I3, In. Ejemplo:



Operaciones de matrices:

- Suma: para suma o resta de matrices, hay que tener en cuenta que al efectuar la suma o la resta a las dos matrices sean de igual tamaño en fila y columna. Ejemplo:




- Multiplicación por un escalar: Es un número o una variable con valor cualquiera que multiplica a una matriz. Ejemplo:


- Matriz Traspuesta: es la inversa de la matriz, es decir, las filas pasan a ser columnas. Por ejemplo:

Esta matriz de 3 filas * 7 columnas pasa ser de 7 filas* 3 columnas







- Multiplicación de matrices: Para la multiplicación de matrices, es necesario analizar las matrices para que al multiplicar que contenga en una matriz el mismo tamaño de columna a la fila de otra matriz. Para la multiplicación es coger la primera fila de la primera matriz y multiplicarlo por la columna de la segunda matriz. Por ejemplo:

Propiedades:

1, A(BC) = (AB)C
2. A(B+C) = AB + AC
3. (A+B)C = AC+BC


Ecuaciones Matriciales:  Ax = b
Una matriz que multiplica a x e iguala los valores de b. Para hallar el valor de ecuación mediante sustitución, igualación o reducción. Por ejemplo:

Al convertir estas matrices en ecuaciones quedaría:
x + 2y -3z = 4
x + 3y +z  = 11
2x+5y-4z  = 13
2x+6y + z = 22



Reducción por Gauss Jordan
El objetivo de este método es procurar que la diagonal principal sea 1 y los otros valores 0 mediante suma, resta, división, es decir convertir la matriz, a una matriz binaria o una matriz identidad. Por ejemplo:


Solución de Sistemas de ecuaciones lineales por Gauss Jordan
A comparación con la reducción de Gauss Jordan, esta se encarga de extraer los coeficientes de las variables de dos o varias ecuaciones, y resolver el ejercicio mediante suma, resta, división, transformando las ecuaciones en una matriz identidad:

A continuación se encontrará un vídeo donde el cual se hará un poco mas explícito este tema:

O puede dar el caso en que a resolver una matriz una fila se igual a 0 pero el resultado sea diferente de 0 es decir que no se puede resolver la matriz

Bibliografia

http://sauce.pntic.mec.es/~jpeo0002/Archivos/PDF/T07.pdf
http://campus.cva.itesm.mx/nazira/Tc1003/PDF/TODO/0701_Tc1003_TODO_Grafos.pdf
http://es.slideshare.net/naborchirinos/conceptos-teoria-de-grafos-5778778
http://www.aulamatematica.com/BC2/08_Matrices_Det/Solo/Determ_Propiedades.pdf

Bienvenidos

Buenos
...Días, Tarde, Noche...

En la parte de arriba encontrará una barra en la cual le indicará opciones para elegir y aprender estos temas

Bienvenidos a esta plataforma; no es una pagina para desperdiciar sino aprovechar la oportunidad de poder aprender un curso básico del Álgebra Lineal; en esta sección van a ver en lo que son Sistemas de ecuaciones lineales, matrices, teoría de grafos, y métodos para resolver ecuaciones lineales, matrices, teoría de grafos, determinantes, etc...

Ecuaciones lineales

Que es: 

Se denomina una Ecuación Lineal ya que tiene forma de polinomio de primer grado, y ninguna incógnita esta elevada a potencia.

Ejemplo: 4x +6y +4z = 5 ... Ecuación que contiene 3 incógnitas. 

En un sistema de ecuación lineal contiene n filas y m columna (en este caso vamos a ver un sistema de 2*2 y de 3*3); y esto a su vez representa un recta en el plano. Resolver un sistema representa que dos ecuaciones se puedan resolver de igual manera: para esto vamos a ver 4 tipos de métodos para solucionar un sistema de ecuación lineal de 2*2:

Reducción:
-Consiste en multiplicar las ecuaciones de modo que se pueda en la resta poder cancelar una variable de la cual al hallar su valor remplazar en una de las ecuaciones para hacer el valor de la otra variable


Sustitución:
- En dos ecuaciones, coger cualquiera de las dos e igualarla 
ejemplo:  
x + 3y = 6
 x - 4y = 7 ------> x = 7 + 4y

- En la primera ecuación reemplazo el valor de x, es decir:  7 + 4y  + 3y = 6
- Resuelve el problema : y = 13/7
- Reemplazo el valor de y en cualquiera de las dos ecuaciones y hallar el valor de x : 
x + 3(13/7) = 6
- Resuelve el problema de la ecuación: x + 39/7 = 6 ----> x = 6 + 39/7 ----> x = 81/7

Igualación:
- Similar al ejercicio anterior pero en este caso con las dos ecuaciones es decir:
x + 3y = 6 -----> x = 6 - 3y
x - 4y = 7 -----> x = 7 + 4y
- Iguala las dos ecuaciones por x ------> x = x ---------> 6 - 3y = 7 + 4y 
- Resuelve el problema: y = 13/7
- Reemplazo el valor de y en cualquiera de las dos ecuaciones; en este caso reemplazaré en la primera ecuación = x + 3(13/7) = 6 ----> x = 81/7

Método gráfico:
- Consiste en igualar las variables a 0 en ambas ecuaciones y ubicar el resultado en el plano cartesiano
(1) x + 3y = 6  ------> 0 + 3y = 6 --> y = 2 ---- x + 0 = 6 -----> x = 6
(2) x - 4y = 7 -------> 0 - 4y = 7 --> y = -7/4 ---- x - 0 = 7 ----> x = 7

(1)       (2) 
x y     x  y
0 2     0  -7/4
6 0     7  0